For $n > 1$, the classic Toffoli $n$-gate is the gate that computes the function from $(\ZZ_2)^n$ into $(\ZZ_2)^n$ given by $$(x_1, \dots, x_n) \mapsto (x_1, \dots, x_{n-1}, x_n \oplus (x_1\cdots x_{n-1})).$$ Note that the classic Toffoli 2-gate is CNOT.
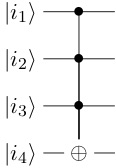
The quantum Toffoli $n$-gate is the unique $n$-qubit gate that maps the computational basis state $|i_n \dots i_1\rangle$ to the computational basis state $|(i_n \oplus i_1 \cdots i_{n-1}) i_{n-1} \dots i_1\rangle$. So quantum CNOT is the quantum Toffoli 2-gate; and here is the quantum Toffoli 4-gate:
The effect of the Toffoli $n$-gate on the set of all computational basis states is that of the following transposition: switch $|01\dots1\rangle$ with $|1\dots11\rangle$ and leave all other computational basis states the same.
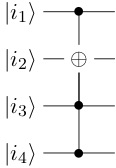
More generally, let $k \in {1, \dots, n}$. The Toffoli gate $T^{(n)}_k$ is the $n$-gate obtained from the Toffoli $n$-gate after switching the $k$th and $n$th wires in the diagram:
So the effect of the Toffoli gate $T^{(n)}_k$ on the set of all computational basis states is the transposition that switches $|1\dots1\rangle$ with $|1\dots101\dots1\rangle$ (where the 0 is the $k$th digit in the label of the second state) and leaves all other computational basis states the same.
Lemma 1
Let $|i_n\dots i_1\rangle$ be any one of the computational basis states and $k \in \{1, \dots, n\}$. Then there exists an $n$-gate $T^{|i_n \dots i_1\rangle}_k$, built from $T^{(n)}_k$ and the Pauli $X$ gates, that switches the states $|i_n\dots i_{k+1} i_k i_{k-1} \dots i_1\rangle$ and $|i_n \dots i_{k+1}\ (i_k \oplus 1)\ i_{k-1} \dots i_1\rangle$, i.e., that flips the $k$th digit in the labels of these two states, and that leaves all other computational basis states the same.
Proof. For $l \in \{1, \dots, n\}$, we denote by $X_l$ the $n$-gate $I_{l-1} \otimes X \otimes I_{n-l}$, that is, the $n$-gate obtained by applying the Pauli $X$ gate to the $l$-th qubit. Let $I$ be the set of all $l \in \{1, \dots, n\}$ such that $l \ne k$ and $i_l = 0$. Then we first apply the product $\Pi_{j \in I} X_j$, changing each $i_j$ with $j \in I$ to 1. Then apply $T^{(n)}_k$. Follow this again by the product $\Pi_{j \in I} X_j$, changing each $i_j$ with $j \in I$ back to 0. Since $T^{(n)}_k$ only switches the basis states $|1\cdots101\cdots 1\rangle$ and $|1\cdots1\rangle$, the resulting circuit only switches the states $|i_n\dots i_{k+1} i_k i_{k-1} \dots i_1\rangle$ and $|i_n \dots i_{k+1}\ (i_k \oplus 1)\ i_{k-1} \dots i_1\rangle$. $\qed$
Lemma 2
Let $|i_n\dots i_1\rangle$ and $|j_n\dots j_1\rangle$ be any two computational basis states. Then there exists and $n$-gate $T^{|i_n\dots i_1\rangle}_{|j_n\dots j_1\rangle}$ that switches $|i_n\dots i_1\rangle$ and $|j_n\dots j_1\rangle$ and leaves all other computational basis states the same.
Proof. Let $l \in \{1, \dots, n\}$ and $1 \le p_1 < p_2 < \cdots < p_l \le n$ be such that $i_{p_q} \ne j_{p_q}$ for each $q=1, \dots, l$, while $i_p = j_p$ for all other indices $p$. We start by applying $T^{|i_n \dots i_1\rangle}_{p_1}$, then $T^{|i_n \dots i_{p_1+1} j_{p_1} i_{p_1-1} \dots i_1\rangle}_{p_2}$, then continuing in this way until finally applying $T^{|i_n \dots i_{p_{l-1}+1} j_{p_{l-1}} i_{p_{l-1}-1} \dots i_{p_1+1} j_{p_1} i_{p_1-1} \dots i_1\rangle}_{p_l}$. At this point, the state $|i_n \dots, i_1\rangle$ has been moved to the state $|j_n \dots j_1\rangle$, but the latter has not yet been moved to the former, only to $|i_n \dots i_{p_{l-1}+1} j_{p_{l-1}} i_{p_{l-1}-1} \dots i_{p_1+1} j_{p_1} i_{p_1-1} \dots i_1\rangle$. To move it all the way to $|i_n \dots i_1\rangle$, we apply again the remaining operators from before, except for the last one, in reverse order: $T^{|i_n \dots i_{p_{l-2}+1} j_{p_{l-2}} i_{p_{l-2}-1} \dots i_{p_1+1} j_{p_1} i_{p_1-1} \dots i_1\rangle}_{p_{l-1}}$ followed by $\dots$ followed by $T^{|i_n \dots i_1\rangle}_{p_1}$. This “going back down the ladder” also has the effect that all the other states are put back into their original place, as required. $\qed$
For notational simplicity, we also denote the compositional basis states by $|0\rangle, \dots, |2^n-1\rangle$ and the Toffoli gates from Problem 2 by $T^{|k\rangle}_{|l\rangle}$, for $k,l \in {0, \dots, 2^n-1}$.
Exercise. Let $k,l \in \{0, \dots, 2^n-1\}$.
- What is the matrix representation of $T^{|k\rangle}_{|l\rangle}$ with respect to the computational basis?
- Let $U$ be a quantum $n$-gate. What is the effect on the matrix representation of $U$ (with respect to the computational basis) of multiplying $U$ by $T^{|k\rangle}_{|l\rangle}$ on the right? On the left?
For the sake of completeness, we also convene that $T^{|k\rangle}_{|k\rangle} = I_{2^n}$, for $k \in {1, \dots, 2^n}$.