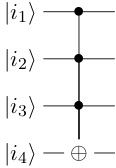
Fix a number $n$ of qubits. In this post, we show how to build the Toffoli gates $T^{|k\rangle}_{|l\rangle}$ out of 1-gates and the CNOT gate. When combined with this post, we conclude that the set of 1-gates together with CNOT form a universal set of quantum gates.
Since $T^{|k\rangle}_{|l\rangle}$ is built from the Pauli gate $X$ and the Toffoli gates $T^{(n)}_k$ (as in Figure 2), it is enough to show that each $T^{(n)}_k$ can be built from CNOT and 1-gates. By the symmetry of wire switching, it is therefore even enough to show that each Toffoli $n$-gate (see the figure for $n=4$) can be built from CNOT and 1-gates.
Lemma 1
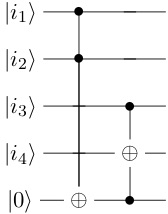
If $n \ge 4$, there is a quantum circuit, with $n-3$ ancillary qubits and consisting only of Toffoli 3-gates, to compute the Toffoli $n$-gate.
Proof. One verifies, by computing the outputs for each computational basis state input, that the following circuit computes the Toffoli 4-gate:
If $n > 4$, we insert after the first Toffoli 3-gate another Toffoli 3-gate with control qubits $|i_3\rangle$ and the first ancillary qubit, and with target qubit the second ancillary qubit; and if $n > 5$, we insert after the last one another Toffoli 3-gate with control qubits $|i_4\rangle$ and the second ancillary qubit, and with target qubit the third ancillary qubit; etc. The last Toffoli 3-gate is the one with control qubits $|i_{n-1}\rangle$ and the last ancillary qubit, and with target qubit $|i_n\rangle$. $\qed$
By Lemma 1, we only need to build the Toffoli 3-gate from CNOT and 1-gates.
Lemma 2
Let $U$ be a 1-gate. Then we can build the 3-gate c-c-$U^2$ using only 1-gates and CNOT.
Proof. One verifies, by computing the outputs for each computational basis state input, that the following circuit computes c-c-$U^2$:
By Corollary 4.2.1 of the book, both c-$U$ and c-$U^\dagger$ can, in turn, be built using only 1-gates and CNOT. This proves the lemma. $\qed$
Lemma 3
There exists a 1-gate $U$ such that $U^2 = X$.
Proof. Direct computation shows that we can take $U = \frac12\begin{pmatrix} 1+i & 1-i \\ 1-i & 1+i \end{pmatrix}$. $\qed$
We denote the 1-gate obtained in Problem 11 as $\sqrt{X}$. Since the Toffoli 3-gate is just c-c-$X$, we conclude:
Corollary
The Toffoli 3-gate can be built using $\sqrt{X}$ and CNOT. $\qed$
Combining the corollary with Lemma 1 and this post, we have now proved the following special case of Theorem 4.4.3 of the book:
Theorem
Every $n$-gate can be built from 1-gates and CNOT. $\qed$