Contents

function out = keen_2000()

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% This code simulates the Keen model as specified
% S. Keen. The nonlinear economics of debt deflation.
% In W. A. Barnett, editor, Commerce, complexity, and evolution: Topics in economics, finance, marketing, and management.
% Proceedings of the Twelfth International Symposium in Economic Theory and Econometrics, pages 83–110, New York, NY, USA, 2000.
% Cambridge University Press.
%
%
% author: M. Grasselli
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
close all
clc
warning on

Parameters attribution and function definitions

% Base parameters - private communication with S. Keen
par_alpha = 0.025;       % productivity growth rate
par_beta = 0.02;         % population growth rate
par_gamma = 0.01;        % depreciation rate
par_nu = 3;              % capital-to-output ratio
par_r = 0.03;            % real interest rate

% Phillips curve - Table 5.1 and private communication with S. Keen
% Phi(lambda) = exp(A+B*lambda)+C
par_A = -57.911;
par_B = 56.162;
par_C = -0.00956;
fun_Phi = @(x) exp(par_A+par_B.*x)+par_C;
fun_Phi_inv = @(y) (log(y-par_C)-par_A)./par_B;

% Modified Phillips curve - used in Keen (1995)
% Phi(lambda) = A/(B-lambda)^2-D
par_A_mod = 0.0000641;
par_B_mod = 1;
par_C_mod = 0.0400641
fun_Phi_mod = @(x) par_A_mod./(par_B_mod-x).^2- par_C_mod;
fun_Phi_mod_inv = @(y) par_B_mod - sqrt(par_A_mod./(y+par_C_mod)); % inverse of Phillips curve


% Investment function - Table 5.1 and private communication with S. Keen
% kappa(pi) = exp(D+E*pi)+F
par_D = -5 ;         % investment function parameter
par_E = 20;          % investment function parameter
par_F = -0.0065;     % investment function parameter
fun_kappa = @(x) min(1,exp(par_D+par_E.*x)+par_F);  % Investment function should have been capped at 1 to prevent consumption going negative
fun_kappa_inv = @(y) (log(y-par_F)-par_D)./par_E;

% Government subsidies - Table 5.1 and private communication with S. Keen
% Gamma(lambda) = exp(G+H*lambda)+I
par_G = 13.5;
par_H = -18.5;
par_I = -0.018;
fun_Gamma = @(x) exp(par_G+par_H*x)+par_I;

% Taxation - Table 5.1 and private communication with S. Keen
% Theta(pi_n) = exp(J+K*pi_n)+L
par_J = -4.465;
par_K = 8.368;
par_L = -0.027;
fun_Theta = @(x) exp(par_J+par_K*x)+par_L;

% Other definitions
TOL = 1E-7;
options = odeset('RelTol', TOL);
txt_format = '%3.3g';

par_C_mod =

    0.0401

Perturbation analysis, page 93

% Equilibrium values

lambda_eq = fun_Phi_inv(par_alpha)                                            % (5.19)
pi_eq = fun_kappa_inv(par_nu*(par_alpha+par_beta+par_gamma))                  % (5.20)
d_eq = (par_nu*(par_alpha+par_beta+par_gamma)-pi_eq)/(par_alpha+par_beta)     % (5.21)
omega_eq = 1-pi_eq-par_r*d_eq

% Stability near equilibrium

omega0 = 0.81;                           % initial wage share from Figure 5.2
lambda0 = 0.94;                          % initial employment rate from Figure 5.2
d0 = 0.04;                               % initial debt ratio from Figure 5.2

y0 = [convert([omega0, lambda0]),d0];

T = 80;

par1 = [par_nu,par_alpha,par_beta,par_gamma,par_r,par_A,par_B,par_C,par_D,par_E,par_F];

% This uses the function 'keen' defined below to simulate the trajectories
% of the Keen model as defined in equation (5.17), page 92
[tK,yK] = ode15s(@(t,y) keen(y,par1), [0 T], y0, options);
yKnew = retrieve([yK(:,1),yK(:,2)]);
yK(:,1) = yKnew(:,1);
yK(:,2) = yKnew(:,2);

% Figure 5.2 in the paper
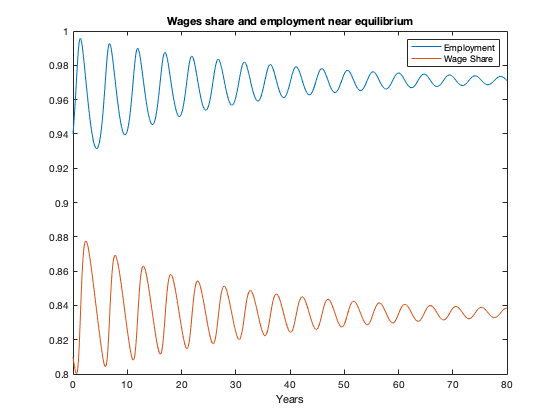
figure(1)
plot(tK, yK(:,2),tK,yK(:,1))
xlabel('Years')
legend('Employment','Wage Share')
title(['Wages share and employment near equilibrium'])

% Figure 5.3 in the paper
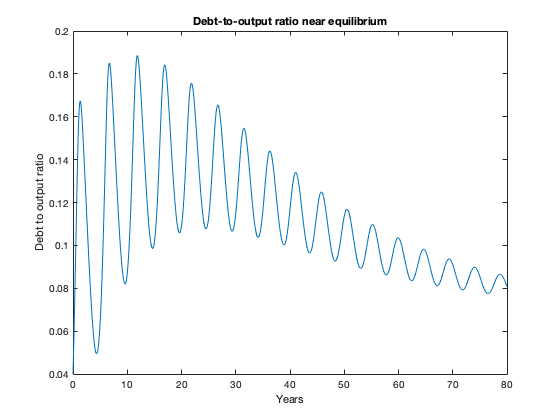
figure(2)
plot(tK, yK(:,3))
xlabel('Years')
ylabel('Debt to output ratio')
title(['Debt-to-output ratio near equilibrium'])


% Figure 5.4 in the paper
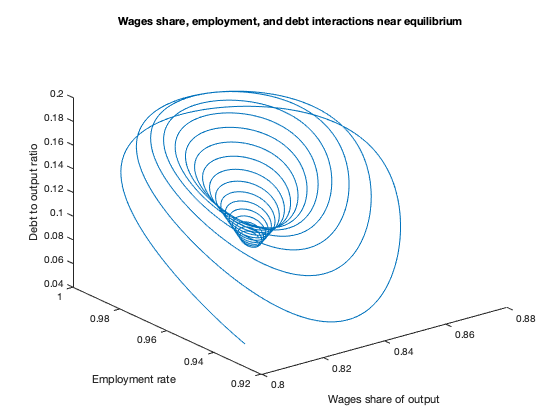
figure(3)
plot3(yK(:,1),yK(:,2),yK(:,3))
xlabel('Wages share of output')
ylabel('Employment rate')
zlabel('Debt to output ratio')
title(['Wages share, employment, and debt interactions near equilibrium'])

% Figure 5.5 in the paper
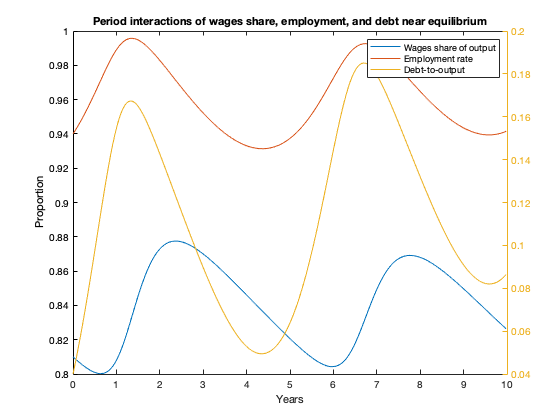
figure(4)
N=max(find(tK<=10));
plot(tK(1:N), yK(1:N,1),tK(1:N),yK(1:N,2))
xlabel('Years')
ylabel('Proportion')
yyaxis('right')
ylabel('Debt-to-output ratio')
plot(tK(1:N), yK(1:N,3))
legend('Wages share of output','Employment rate','Debt-to-output')
title(['Period interactions of wages share, employment, and debt near equilibrium'])

% Instability away from equilibrium - first example
% Note: this example does not work with the Phillips curve in exponential
% form suggested in this paper, but works with the modified Phillips used
% in Keen (1995)

% Modified Equilibrium values

lambda_eq_mod = fun_Phi_mod_inv(par_alpha);

omega0 = omega_eq-0.11;                  % initial wage share, page 95
lambda0 = lambda_eq_mod-0.05;            % initial employment rate, page 95
d0 = d_eq;                               % initial debt ratio, page 95

y0 = [convert([omega0, lambda0]),d0];

T = 100;

% par2 = [par_nu,par_alpha,par_beta,par_gamma,par_r,par_A,par_B,par_C,par_D,par_E,par_F];
par2_mod = [par_nu,par_alpha,par_beta,par_gamma,par_r,par_A_mod,par_B_mod,par_C_mod,par_D,par_E,par_F];

% This uses the function 'keen_mod' defined below to simulate the
% trajectories of the Keen model as specified in equation (5.17), page 92,
% but with the modified Phillips curve used in Keen (1995) instead of the
% one provided in Table 5.1
% [tK,yK] = ode15s(@(t,y) keen(y,par2), [0 T], y0, options);
[tK,yK] = ode15s(@(t,y) keen_mod(y,par2_mod), [0 T], y0, options);
yKnew = retrieve([yK(:,1),yK(:,2)]);
yK(:,1) = yKnew(:,1);
yK(:,2) = yKnew(:,2);

% Figure 5.6 in the paper
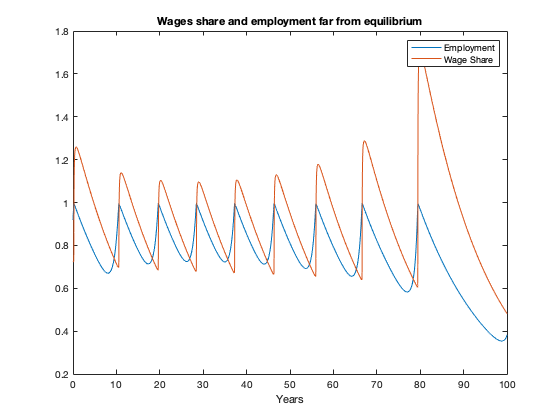
figure(5)
plot(tK, yK(:,2),tK,yK(:,1))
xlabel('Years')
legend('Employment','Wage Share')
title(['Wages share and employment far from equilibrium'])

% Figure 5.7 in the paper
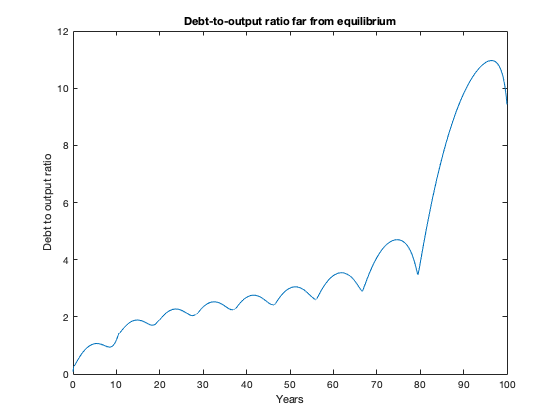
figure(6)
plot(tK, yK(:,3))
xlabel('Years')
ylabel('Debt to output ratio')
title(['Debt-to-output ratio far from equilibrium'])


% Figure 5.8 in the paper
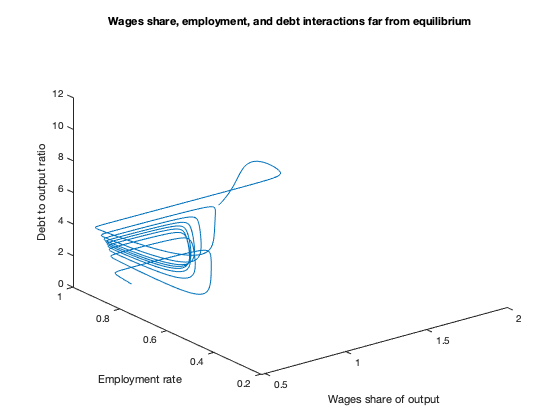
figure(7)
plot3(yK(:,1),yK(:,2),yK(:,3))
xlabel('Wages share of output')
ylabel('Employment rate')
zlabel('Debt to output ratio')
title(['Wages share, employment, and debt interactions far from equilibrium'])

% Figure 5.9 in the paper
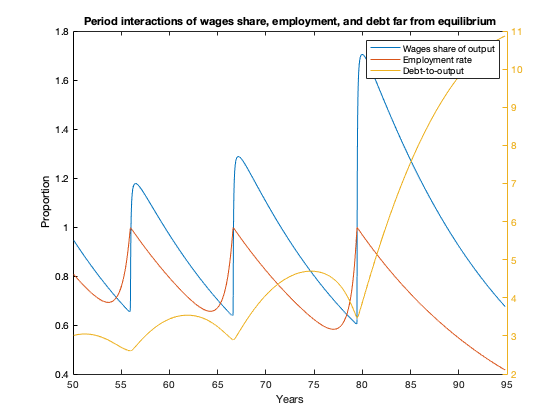
figure(8)
N_min=min(find(tK>50));
N_max=max(find(tK<=95));
plot(tK(N_min:N_max), yK(N_min:N_max,1),tK(N_min:N_max),yK(N_min:N_max,2))
xlabel('Years')
ylabel('Proportion')
yyaxis('right')
ylabel('Debt-to-output ratio')
plot(tK(N_min:N_max), yK(N_min:N_max,3))
legend('Wages share of output','Employment rate','Debt-to-output')
title(['Period interactions of wages share, employment, and debt far from equilibrium'])

lambda_eq =

    0.9712


pi_eq =

    0.1618


d_eq =

    0.0702


omega_eq =

    0.8361

Adding a government sector, page 100

% Low interest (r = 3%)

% par3 = [par_nu,par_alpha,par_beta,par_gamma,par_r,par_A,par_B,par_C,par_D,par_E,par_F...
%    par_G,par_H,par_I,par_J,par_K,par_L];
par3_mod = [par_nu,par_alpha,par_beta,par_gamma,par_r,par_A_mod,par_B_mod,par_C_mod,par_D,par_E,par_F...
    par_G,par_H,par_I,par_J,par_K,par_L];

% New equilibrium values, footnote 10

% This uses the Phillips curve in Table 5.1, which is NOT used in the
% simulations, because it does not work
lambda_eq = fun_Phi_inv(par_alpha)                                           % Same as (5.19)
pi_eq = fun_kappa_inv(par_nu*(par_alpha+par_beta+par_gamma))                 % Same as (5.20)
g_eq = fun_Gamma(lambda_eq)/(par_alpha+par_beta)                             % Derived from equation 4 in (5.27)
t_eq = fun_Theta(pi_eq)/(par_alpha+par_beta)                                 % Derived from equation 5 in (5.27)
d_eq = (par_nu*(par_alpha+par_beta+par_gamma)-pi_eq)/(par_alpha+par_beta)    % Derived from equation 3 in (5.27)
omega_eq = 1-pi_eq-par_r*d_eq-t_eq+g_eq
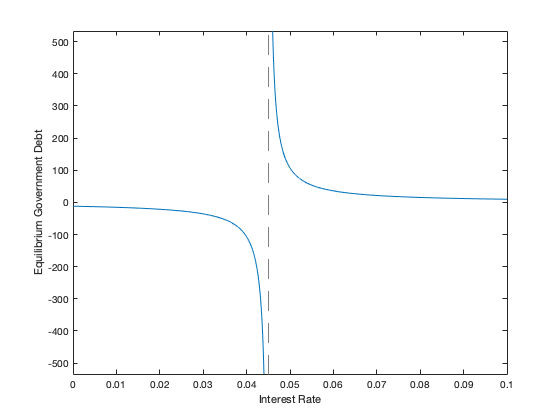
d_g_eq=(t_eq-g_eq)/(par_r-par_alpha-par_beta)

% Figure 5.10 in the paper
figure(9)
z=[];
syms d_g(z)
d_g(z) = (t_eq-g_eq)/(z-par_alpha-par_beta);
fplot(d_g,[0,0.1]);
xlabel('Interest Rate')
ylabel('Equilibrium Government Debt')

% initial values, footnote 10
omega0 = 0.31;
lambda0 = 0.98;
dk0 = 0.08;
dg0 = -36;
g0 = -0.13;
t0 = 0.4;

y0 = [convert([omega0, lambda0]),dk0,dg0,g0,t0];

T = 200;

% This uses the function 'keen_government' defined below to simulate the
% trajectories of the Keen model with government subisidies and taxes as
% defined in equation (5.27), pages 100-101, but with the modified Phillips
% curve used in Keen (1995) instead of the one provided in Table 5.1
[tK,yK] = ode15s(@(t,y) keen_government(y,par3_mod), [0 T], y0, options);
yKnew = retrieve([yK(:,1),yK(:,2)]);
yK(:,1) = yKnew(:,1);
yK(:,2) = yKnew(:,2);


% Figure 5.11 in the paper
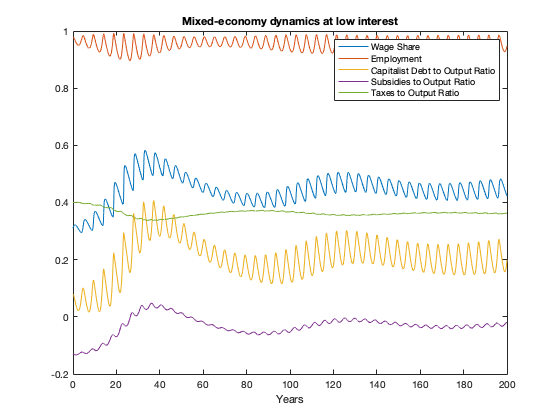
figure(10)
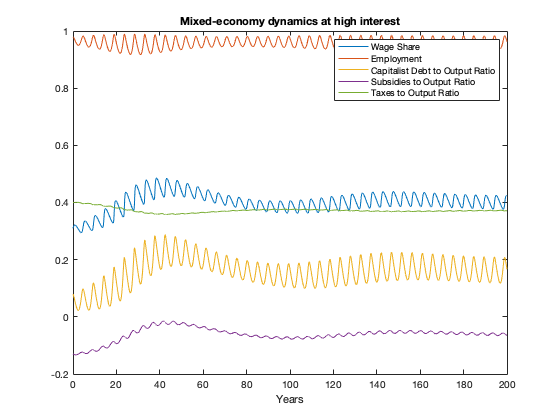
plot(tK, yK(:,1),tK,yK(:,2),tK,yK(:,3),tK,yK(:,5),tK,yK(:,6))
xlabel('Years')
legend('Wage Share','Employment','Capitalist Debt to Output Ratio','Subsidies to Output Ratio','Taxes to Output Ratio')
title(['Mixed-economy dynamics at low interest'])

% Figure 5.12 in the paper
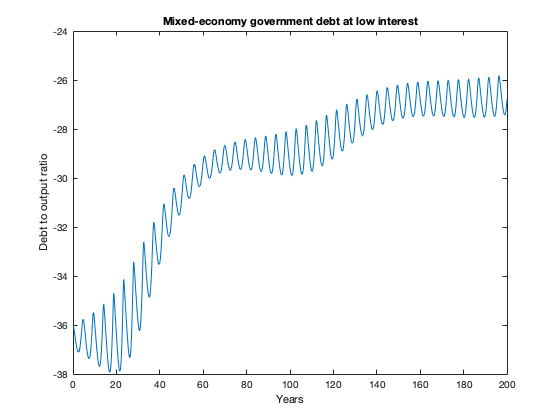
figure(11)
plot(tK, yK(:,4))
xlabel('Years')
ylabel('Debt to output ratio')
title(['Mixed-economy government debt at low interest'])

% Figure 5.13 in the paper
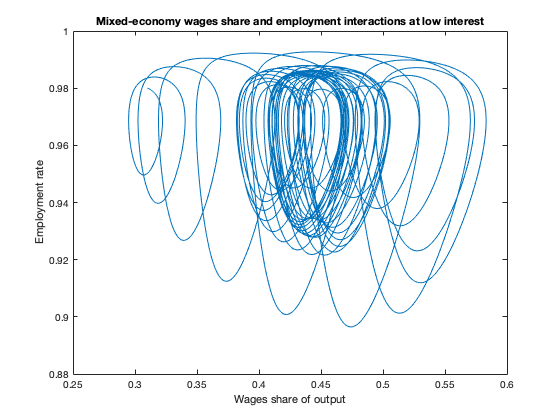
figure(12)
plot(yK(:,1),yK(:,2))
xlabel('Wages share of output')
ylabel('Employment rate')
title(['Mixed-economy wages share and employment interactions at low interest'])

% High interest (r=5%)

par_r = 0.05;

par4_mod = [par_nu,par_alpha,par_beta,par_gamma,par_r,par_A_mod,par_B_mod,par_C_mod,par_D,par_E,par_F...
    par_G,par_H,par_I,par_J,par_K,par_L];

% initial values, footnote 10
omega0 = 0.31;
lambda0 = 0.98;
dk0 = 0.08;
dg0 = 110;
g0 = -0.13;
t0 = 0.4;

y0 = [convert([omega0, lambda0]),dk0,dg0,g0,t0];

T = 200;

% This uses the function 'keen_government' defined below to simulate the
% trajectories of the Keen model with government subisidies and taxes as
% defined in equation (5.27), pages 100-101, but with the modified Phillips
% curve used in Keen (1995) instead of the one provided in Table 5.1
[tK,yK] = ode15s(@(t,y) keen_government(y,par4_mod), [0 T], y0, options);
yKnew = retrieve([yK(:,1),yK(:,2)]);
yK(:,1) = yKnew(:,1);
yK(:,2) = yKnew(:,2);


% Not shown in the paper, but coincides with Figure 5.11 in the paper
figure(13)
plot(tK, yK(:,1),tK,yK(:,2),tK,yK(:,3),tK,yK(:,5),tK,yK(:,6))
xlabel('Years')
legend('Wage Share','Employment','Capitalist Debt to Output Ratio','Subsidies to Output Ratio','Taxes to Output Ratio')
title(['Mixed-economy dynamics at high interest'])

% Figure 5.14 in the paper
figure(14)
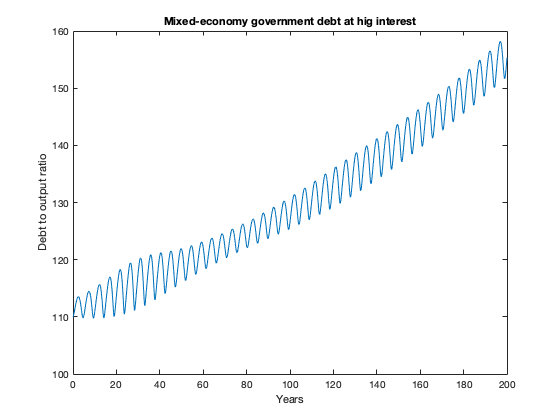
plot(tK, yK(:,4))
xlabel('Years')
ylabel('Debt to output ratio')
title(['Mixed-economy government debt at hig interest'])

% Figure 5.15 in the paper
figure(15)
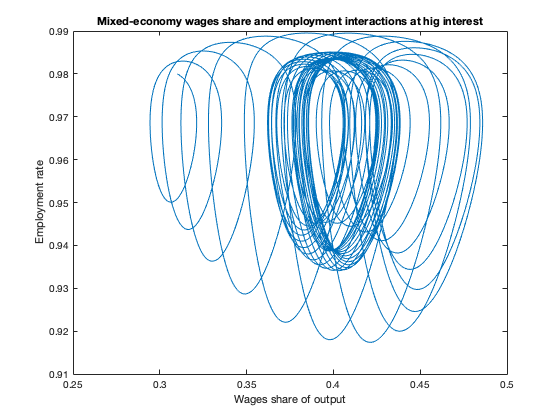
plot(yK(:,1),yK(:,2))
xlabel('Wages share of output')
ylabel('Employment rate')
title(['Mixed-economy wages share and employment interactions at hig interest'])

lambda_eq =

    0.9712


pi_eq =

    0.1618


g_eq =

   -0.1450


t_eq =

    0.3904


d_eq =

    0.0702


omega_eq =

    0.3006


d_g_eq =

  -35.6965

Auxiliary functions

% Instead of integrating the system in terms of omega, lambda and d, we
% decided to use:
%
% log_omega = log(omega),
% tan_lambda = tan((lambda-0.5)*pi), and
% pi_n=1-omega-r*d
% log_p = log(p)
%
% Experiments show that the numerical methods work better with
% these variables.

function new = convert(old,r)
    % This function converts
    % [omega, lambda, d, p]
    % to
    % [log_omega, tan_lambda, pi_n, log_p]
    % It also work with the first 2 or 3 elements alone.
    % each of these variables might also be a time-dependent vector

    n = size(old,2); %number of variables
    new = zeros(size(old));

    new(:,1) = log(old(:,1));
    new(:,2) = tan((old(:,2)-0.5)*pi);
    if n>2
        new(:,3) = 1-old(:,1)-r*old(:,3);
        if n==4
            new(:,4) = log(old(:,4));
        end
    end
end

function old = retrieve(new,r)
    % This function retrieves [omega, lambda, d, p]
    % from
    % [log_omega, tan_lambda, pi_n, log_p]
    %
    %  It also work with the first 2 or 3 elements alone.
    % each of these variables might also be a time-dependent vector

    n = size(new,2); %number of variables
    old = zeros(size(new));

    old(:,1) = exp(new(:,1));
    old(:,2) = atan(new(:,2))/pi+0.5;
    if n>2
        old(:,3) = (1-old(:,1)-new(:,3))/r;
        if n==4
            old(:,4) = exp(new(:,4));
        end
    end
end


function f = keen(y,par)
    f = zeros(3,1);
    log_omega = y(1);
    tan_lambda = y(2);
    d = y(3);
    lambda = atan(tan_lambda)/pi+0.5;   % pi = 3.14 here
    omega = exp(log_omega);

    nu = par(1);
    alpha = par(2);
    beta = par(3);
    gamma = par(4);
    r = par(5);

    A = par(6);
    B = par(7);
    C = par(8);

    D = par(9);
    E = par(10);
    F = par(11);

    pi_n = 1-omega-r*d;
    phillips = exp(A+B*lambda)+C;
    kappa = exp(D+E*pi_n)+F;

    g_Y = kappa/nu-gamma;


    f(1) = phillips-alpha;                                     %d(log_omega)/dt
    f(2) = (1+tan_lambda^2)*pi*lambda*(g_Y-alpha-beta);        %d(tan_lambda)/dt
    f(3) = d*(r-(kappa/nu-gamma))+kappa-(1-omega);             % dd/dt
end


function f = keen_mod(y,par)
    f = zeros(3,1);
    log_omega = y(1);
    tan_lambda = y(2);
    d = y(3);
    lambda = atan(tan_lambda)/pi+0.5;   % pi = 3.14 here
    omega = exp(log_omega);

    nu = par(1);
    alpha = par(2);
    beta = par(3);
    gamma = par(4);
    r = par(5);

    A = par(6);
    B = par(7);
    C = par(8);

    D = par(9);
    E = par(10);
    F = par(11);

    pi_n = 1-omega-r*d;
    phillips = A./(B-lambda)^2- C;
    kappa = exp(D+E*pi_n)+F;

    g_Y = kappa/nu-gamma;


    f(1) = phillips-alpha;                                     %d(log_omega)/dt
    f(2) = (1+tan_lambda^2)*pi*lambda*(g_Y-alpha-beta);        %d(tan_lambda)/dt
    f(3) = d*(r-(kappa/nu-gamma))+kappa-(1-omega);             % dd/dt
end



function f = keen_government(y,par)
    f = zeros(6,1);
    log_omega = y(1);
    tan_lambda = y(2);
    dk = y(3);
    dg = y(4);
    g = y(5);
    t = y(6);

    lambda = atan(tan_lambda)/pi+0.5;   % pi = 3.14 here
    omega = exp(log_omega);

    nu = par(1);
    alpha = par(2);
    beta = par(3);
    gamma = par(4);
    r = par(5);

    A = par(6);
    B = par(7);
    C = par(8);

    D = par(9);
    E = par(10);
    F = par(11);

    G = par(12);
    H = par(13);
    I = par(14);

    J = par(15);
    K = par(16);
    L = par(17);


    pi_n = 1-omega-r.*dk+g-t;
%   phillips = exp(A+B*lambda)+C;
    phillips = A./(B-lambda)^2- C;
    kappa = exp(D+E*pi_n)+F;
    Gamma = exp(G+H*lambda)+I;
    Theta = exp(J+K*pi_n)+L;


    g_Y = kappa/nu-gamma;

    f(1) = phillips-alpha;                                     % d(log_omega)/dt
    f(2) = (1+tan_lambda^2)*pi*lambda*(g_Y-alpha-beta);        % d(tan_lambda)/dt
    f(3) = kappa-(1-omega)+t-g+dk*(r-kappa/nu+gamma);          % dd_k/dt
    f(4) = dg*(r-kappa/nu+gamma)+g-t;                         % dd_g/dt
    f(5) = Gamma - g*(kappa/nu-gamma);                         % dg/dt
    f(6) = Theta - t*(kappa/nu-gamma);                         % d(t)/dt
end

end

Published with MATLAB® R2020a