Logistic Regression for
Classification
2002-04-06
> treedata
obj A B C D E
1 1 y n y n y
2 1 n n y n y
3 1 y n y y y
4 1 n y n n n
5 1 y y n y n
6 1 n n y n y
7 1 n n n n n
8 1 n n n n n
9 0 n n n n y
10 0 y y n n y
11 0 n n y y y
12 0 y y y y n
13 0 n y n y n
14 0 n n n n y
15 0 n n n n y
16 0 n y n n y
17 0 n n n n y
18 0 n y n n y
19 0 n y n n y
20 0 n n n n y
> fittree <- glm(cbind(obj,1-obj)~A+B+C+D+E, data=treedata, family=binomial(link=logit))
> fittree1 <- step(fittree)
Start: AIC= 23.7
cbind(obj, 1 - obj) ~ A + B + C + D + E
Df Deviance AIC
<none> 11.703 23.703
- C 1 14.170 24.170
- A 1 14.208 24.208
- D 1 15.394 25.394
- B 1 15.437 25.437
- E 1 22.426 32.426
> anova(fittree1,test="Chisq")
Analysis of Deviance Table
Model: binomial, link: logit
Response: cbind(obj, 1 - obj)
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
NULL 19 26.9205
A 1 1.0949 18 25.8255 0.2954
B 1 2.2827 17 23.5429 0.1308
C 1 0.5149 16 23.0279 0.4730
D 1 0.6017 15 22.4263 0.4379
E 1 10.7236 14 11.7027 0.0011
> summary(fittree1)
Call:
glm(formula = cbind(obj, 1 - obj) ~ A + B + C + D + E, family = binomial(link = logit),
data = treedata)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.231e+00 -6.366e-01 -7.821e-05 1.997e-01 1.227e+00
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 18.566 89.128 0.208 0.835
Ay 10.235 60.252 0.170 0.865
By -18.112 89.116 -0.203 0.839
Cy 2.517 1.744 1.443 0.149
Dy -10.805 60.250 -0.179 0.858
Ey -20.060 89.118 -0.225 0.822
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 26.920 on 19 degrees of freedom
Residual deviance: 11.703 on 14 degrees of freedom
AIC: 23.703
Number of Fisher Scoring iterations: 10
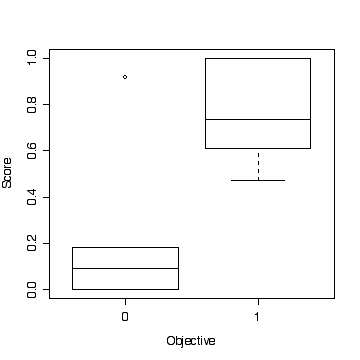
> boxplot(split(invlogit(predict(fittree1)),treedata$obj),
ylab="Score",xlab="Objective")