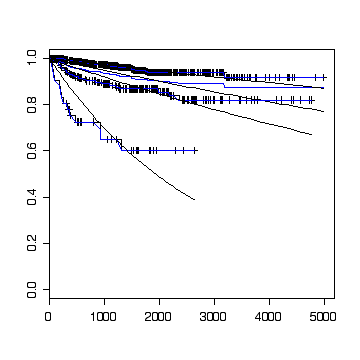
The first calculation uses the library functions survfit and survreg to plot the Kaplan-Meier estimate and perform a regression on tumour size (categorized into three size classes) assuming an exponential distribution of time to relapse.
> library(survival)
> cervical$csize <- cut(cervical$size,br=c(0,10,30,80),incl=T)
> plot(survfit(Surv(etime,event)~csize,data=cervical))
> cervfite <- survreg(Surv(etime, event) ~ csize, data = cervical,
subset = etime > 0 & !is.na(etime) & !is.na(csize), dist="exp")
> summary(cervfite)
Call:
survreg(formula = Surv(etime, event) ~ csize, data = cervical,
subset = etime > 0, dist = "exp")
Value Std. Error z p
(Intercept) 10.50 0.200 52.48 0.00e+00
csize(10,30] -1.10 0.278 -3.97 7.06e-05
csize(30,80] -2.56 0.334 -7.67 1.67e-14
Scale fixed at 1
Exponential distribution
Loglik(model)= -693.1 Loglik(intercept only)= -717
Chisq= 47.71 on 2 degrees of freedom, p= 4.4e-11
Number of Newton-Raphson Iterations: 6
n=844 (59 observations deleted due to missing)
> anova(cervfite)
Df Deviance Resid. Df -2*LL P(>|Chi|)
NULL NA NA 1 1433.923 NA
csize 2 47.7124 3 1386.211 4.358964e-11
Here is a home-made function to plot the Kaplan-Meier curve and fit an exponential distribution.
> plotsurv2
function (eetime, eetype, KM = T, showexp = F, newplot = T, subset = NULL,
...)
{
if (is.null(subset))
subset <- TRUE
etime <- eetime[subset][!is.na(eetime[subset])]
etype <- eetype[subset][!is.na(eetime[subset])]
tord <- order(etime)
etime <- etime[tord]
etype <- etype[tord]
n <- length(etime)
r <- sum(etype)
ni <- n - cumsum(!etype)
if (KM)
frac <- cumprod(1 - etype/(n:1))
else frac <- 1 - cumsum(etype/ni)
if (newplot)
plot(c(0, etime), c(1, frac), type = "l", col = "blue",
xlab = "time", ylab = "P(Survive > time)", ...)
else lines(c(0, etime), c(1, frac), type = "l", col = "blue")
if (showexp) {
muhat <- (n/r) * mean(etime)
tgr <- seq(0, max(etime), length = 60)
lines(tgr, exp(-tgr/muhat))
list(muhat = muhat, logL = -r * (log(muhat) + 1), r = r,
n = n)
}
else invisible()
}
> attach(cervical)
> fit0 <- plotsurv2(etime,event,T,T,F,!is.na(csize))
> fit1 <- plotsurv2(etime,event,T,T,F,as.numeric(csize)==1)
> fit2 <- plotsurv2(etime,event,T,T,F,as.numeric(csize)==2)
> fit3 <- plotsurv2(etime,event,T,T,F,as.numeric(csize)==3)
> fit1$mu
[1] 36177.56
> fit2$mu
[1] 12005.93
> fit3$mu
[1] 2792.429
> log(fit1$mu)
[1] 10.49619
> log(fit2$mu)-log(fit1$mu)
[1] -1.103039
> log(fit3$mu)-log(fit1$mu)
[1] -2.561527
Here is the likelihood ratio chi-square to test the equivalence of the three groups:
> chisq <- -2*(fit0$l-(fit1$l+fit2$l+fit3$l)) > chisq [1] 47.7124
The following calculation applies Bartlett's correction to the likelihood ratio chi-square:
> Cinv <- 1+((1/fit1$r)+(1/fit2$r)+(1/fit3$r)-(1/fit0$r))/12 > Cinv [1] 1.011110 > chisq/Cinv [1] 47.18817 > 1-pchisq(chisq,2) [1] 4.358969e-11 > 1-pchisq(chisq/Cinv,2) [1] 5.665257e-11