STATISTICS 4M03/6M03: Test #2
19 November 2002
Students may bring and use any calculators, tables, books or notes.
[4] 1. Assume that you have a way to generate N(0, 1) variates on the computer. How could you get Np(0, I) random variables? How could you transform them to get Np(m, S) random variables for given vector m and matrix S?
[12] 2. Consider a bivariate distribution uniform over the rectangle defined by vertices (7, 5), (5, 7), (-7, -5), (-5, -7).
Find the mean vector and the covariance matrix. Find and graph the marginal distribution of X. Plot the rectangle, the regression of Y on X and the regression of X on Y. Hint: Find the means and variances for a rectangle with the same dimensions, but centered on the origin and parallel to the axes. If a figure is centered on the origin, it will be rotated 45º counterclockwise around its centre by the transformation
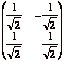
[6] 3. Consider a bivariate normal distribution with the same mean vector and the same covariance matrix as the uniform distribution in Question 2. Add the two regression lines of this normal distribution to the graph you drew in Question 2.
[8] 4. Text Problem 2.9.18, page 53.
[8] 5. Text Problem 2.9.29, page 55.