Statistics 4M03/6M03 - Assignment #2
2001-10-20
Due: 2001-11-12 17:00
You should use Splus or R to do the calculations and draw the graphs.
The numbered Exercises are from Johnson & Wichern, Applied
Multivariate Statistical Analysis, 4th edition.
Part A
Question 1
(a) Draw a perspective plot of the bivariate normal
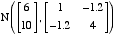
probability density function.
(b) Find and graph the marginal density of X1 and the
conditional density of X1 given X2 =
x2, for x2 = 8, 10, 12.
(c) Plot the ellipses of concentration for 50%, 90%, 95% and 99%
concentration. Add both regression lines to this plot.
Question 2
Repeat Question 1 for a bivariate distribution uniform
on an ellipse, with the same mean and covariance matrix as the
bivariate normal distribution in Question 1.
[Hint: Find the mean and covariance matrix for a random
variable V with distribution uniform on the unit circle
centred at the origin, then find the distribution of X = m + BV, then find what B you need
to give X the specified covariance matrix.]
Question 3
Consider the bivariate density function
f(x1, x2) = x1
(x1 - x2)/8 when 0 < x1 < 2,
-x1 < x2 <x1 and 0 otherwise.
(a) Find and graph the marginal and conditional distributions.
(b) Find and graph the regression of X1 on
X2 and the regression of X2 on X1.
Part B
4.4
4.10 - 4.14
4.35 Also, see if Box-Cox transformations will help to
improve normality.
![]()