Statistics 4C03/6C03 - Test #1
2007-02-12 17:30-19:30
- This test is to be written in the BSB Student Technology Centre. The duration of the test is 2 hours.
- Any aids and resources are permitted. You may consult any web pages but you may not use e-mail or communicate with anyone other than the instructor.
- When no particular method is specified and there is a choice, you are free to use any method you like.
Part A.
Analyse the following two examples. Include an ANOVA table and a 99% confidence interval for the residual variance. State your assumptions and your conclusions.
- The percentage of hardwood concentration in raw pulp,
the freeness and the cooking time of the pulp, were investigated for
their effects on the strength of paper.
| Cooking time 1.5 hr |
|
Freeness |
|
|
350 |
500 |
650 |
| % Hardwood |
10 |
96.6, 96.0 |
97.7, 96.0 |
99.4, 99.8 |
|
15 |
98.5, 97.2 |
96.0, 96.9 |
98.4, 97.6 |
| |
20 |
97.5, 96.6 |
95.6, 96.2 |
97.4, 98.1 |
| Cooking time 2.0 hr |
|
Freeness |
|
|
350 |
500 |
650 |
| % Hardwood |
10 |
98.4, 98.6 |
99.6, 100.4 |
100.6, 100.9 |
|
15 |
97.5, 98.1 |
98.7, 96.0 |
99.6, 99.0 |
| |
20 |
97.6, 98.4 |
97.0, 97.8 |
98.5, 99.8 |
- The following data come from a fractional factorial
design used to study the effect of temperature, pressure,
concentration and stirring rate on filtration rate in a chemical
process.
| run |
temp |
press |
conc |
stir |
filtration |
| 1 |
- |
- |
- |
- |
45 |
| 2 |
+ |
- |
- |
+ |
100 |
| 3 |
- |
+ |
- |
+ |
45 |
| 4 |
+ |
+ |
- |
- |
65 |
| 5 |
- |
- |
+ |
+ |
75 |
| 6 |
+ |
- |
+ |
- |
60 |
| 7 |
- |
+ |
+ |
- |
80 |
| 8 |
+ |
+ |
+ |
+ |
96 |
Part B.
Consider a negative binomial distribution with the following
parameterization:
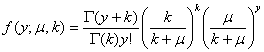
- Show that this distribution is in the exponential family if k
is known, but k is not a dispersion parameter as defined by
McCullagh & Nelder. Find the exponential family components: cumulant
function,
canonical parameter, canonical link, mean, and variance function.
- Here is a vector of 9 observations from this distribution:
yT = (4, 7, 6, 0, 1, 2, 3, 5, 11). Find 95% Wald and
Score confidence intervals for the mean, assuming k = 3.
Estimate k by moments.
- Show that in the limit as k goes to infinity with mu fixed,
this distribution becomes the Poisson. [Hint: You can take the limit
of the probability density function, or you can use the cumulant
function you found in (1) to get the cumulant-generating function in
terms of mu and show that it approaches the Poisson cumulant-generating
function as k goes to infinity.]