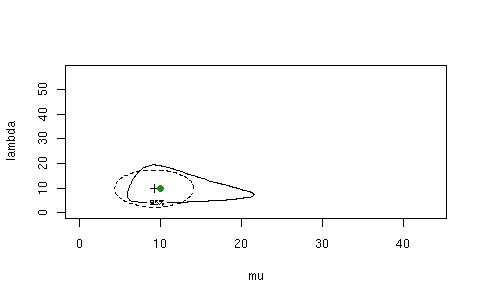
 > IGconfLLRWboot(n=20, mu=10, lambda=10, B=20, conflevel=95, refresh=F)
$"Observed Confidence"
LLRconf Waldconf
90 85
$Crosstab
Waldmiss
LLRmiss FALSE TRUE
FALSE 17 1
TRUE 0 2
> IGconfLLRWboot(n=20, mu=10, lambda=10, B=20, conflevel=95, refresh=F)
$"Observed Confidence"
LLRconf Waldconf
90 85
$Crosstab
Waldmiss
LLRmiss FALSE TRUE
FALSE 17 1
TRUE 0 2
 > IGconfLLRWboot(n=50, mu=1, lambda=100, conflevel=90)
$"Observed Confidence"
LLRconf Waldconf
91 90
$Crosstab
Waldmiss
LLRmiss FALSE TRUE
FALSE 89 2
TRUE 1 8
> IGconfLLRWboot(n=50, mu=1, lambda=100, conflevel=90)
$"Observed Confidence"
LLRconf Waldconf
91 90
$Crosstab
Waldmiss
LLRmiss FALSE TRUE
FALSE 89 2
TRUE 1 8
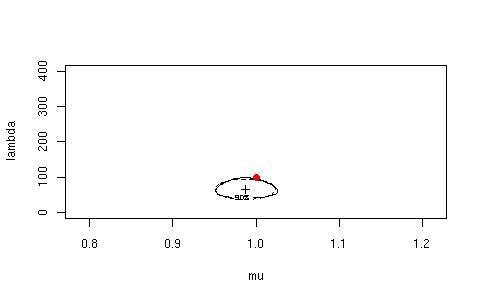 > IGconfLLRWboot(n=50, mu=1, lambda=100, B=1000, conflevel=90)
$"Observed Confidence"
LLRconf Waldconf
88.2 88.6
$Crosstab
Waldmiss
LLRmiss FALSE TRUE
FALSE 871 11
TRUE 15 103
> IGconfLLRWboot(n=50, mu=1, lambda=100, B=1000, conflevel=90)
$"Observed Confidence"
LLRconf Waldconf
88.2 88.6
$Crosstab
Waldmiss
LLRmiss FALSE TRUE
FALSE 871 11
TRUE 15 103
> IGconfLLRWboot function (n, mu, lambda, B = 100, conflevel = 95, refresh = T, ...) { mgr <- seq(max(mu - 15 * sqrt(mu^3/(n * lambda)), 0), mu + 15 * sqrt(mu^3/(n * lambda)), len = 101) lgr <- seq(max(lambda - 15 * lambda * sqrt(2/n), 0), lambda + 15 * lambda * sqrt(2/n), len = 101) LLRmiss <- NULL Waldmiss <- NULL for (BB in 1:B) { xx <- rinvGauss(n, mu, lambda) xbar <- mean(xx) xbar1 <- mean(1/xx) muhat <- xbar lambdahat <- 1/(xbar1 - 1/xbar) LLRout <- neg2LLRIG(mu, lambda, n, xbar, xbar1) > qchisq(conflevel/100, 2) LLRmiss <- c(LLRmiss, LLRout) Waldout <- n * ((mu - muhat)^2 * lambdahat/muhat^3 + (lambda - lambdahat)^2/(2 * lambdahat^2)) > qchisq(conflevel/100, 2) Waldmiss <- c(Waldmiss, Waldout) contour(mgr, lgr, outer(mgr, lgr, neg2LLRIG, n = n, xbar = xbar, xbar1 = xbar1), levels = qchisq(conflevel/100, 2), labels = paste(conflevel, "%", sep = ""), xlab = "mu", ylab = "lambda", add = (!refresh & BB > 1), ...) ellipsem(c(muhat, lambdahat), n * diag(c(lambdahat/muhat^3, 1/(2 * lambdahat^2))), qchisq(conflevel/100, 2), lty = 2) points(muhat, lambdahat, pch = 3) points(mu, lambda, col = c("forestgreen", "yellow", "blue", "red")[1 + 2 * LLRout + Waldout], pch = 16) } list("Observed Confidence" = c(LLRconf = 100 * (B - sum(LLRmiss))/B, Waldconf = 100 * (B - sum(Waldmiss))/B), Crosstab = table(LLRmiss, Waldmiss)) } > ellipsem function (mu, amat, c2, npoints = 100, showcentre = T, ...) { if (all(dim(amat) == c(2, 2))) { eamat <- eigen(amat) hlen <- sqrt(c2/eamat$val) theta <- angle(eamat$vec[1, 1], eamat$vec[2, 1]) ellipse(hlen[1], hlen[2], theta, mu[1], mu[2], npoints = npoints, ...) if (showcentre) points(mu[1], mu[2], pch = 3) } invisible() } > ellipse function (hlaxa = 1, hlaxb = 1, theta = 0, xc = 0, yc = 0, newplot = F, npoints = 100, ...) { a <- seq(0, 2 * pi, length = npoints + 1) x <- hlaxa * cos(a) y <- hlaxb * sin(a) alpha <- angle(x, y) rad <- sqrt(x^2 + y^2) xp <- rad * cos(alpha + theta) + xc yp <- rad * sin(alpha + theta) + yc if (newplot) plot(xp, yp, type = "l", ...) else lines(xp, yp, ...) invisible() } > angle function (x, y) { angle2 <- function(xy) { x <- xy[1] y <- xy[2] if (x > 0) { atan(y/x) } else { if (x < 0 & y != 0) { atan(y/x) + sign(y) * pi } else { if (x < 0 & y == 0) { pi } else { if (y != 0) { (sign(y) * pi)/2 } else { NA } } } } } apply(cbind(x, y), 1, angle2) }