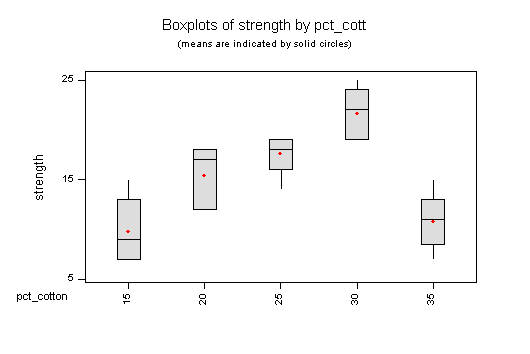

(Note that for exam purposes, a comparative dot plot would be better than a comparative box plot.)
One-way Analysis of Variance
Analysis of Variance for strength
Source DF SS MS F P
pct_cott 4 475.76 118.94 14.76 0.000
Error 20 161.20 8.06
Total 24 636.96
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ------+---------+---------+---------+
15 5 9.800 3.347 (-----*----)
20 5 15.400 3.130 (----*----)
25 5 17.600 2.074 (----*----)
30 5 21.600 2.608 (----*----)
35 5 10.800 2.864 (-----*----)
------+---------+---------+---------+
Pooled StDev = 2.839 10.0 15.0 20.0 25.0
95% Confidence interval for s2: (4.72, 16.8)
Conclusions:
There is strong evidence (P < 0.001) that % cotton affects the mean strength. The highest mean strength was at 30% cotton. Further trials around 30% cotton may help find the % cotton that gives the highest strength.
Assumptions:
Independent observations; variation in strength follows a normal distribution with the same variance at each level of % cotton.
Regression Analysis The regression equation is strength = 10.9 + 0.164 pct_cotton Predictor Coef StDev T P Constant 10.940 3.764 2.91 0.008 pct_cott 0.1640 0.1449 1.13 0.269 S = 5.122 R-Sq = 5.3% R-Sq(adj) = 1.2% Analysis of Variance Source DF SS MS F P Regression 1 33.62 33.62 1.28 0.269 Residual Error 23 603.34 26.23 Lack of Fit 3 442.14 147.38 18.29 0.000 Pure Error 20 161.20 8.06 Total 24 636.96 Unusual Observations Obs pct_cott strength Fit StDev Fit Residual St Resid 21 35.0 7.00 16.68 1.77 -9.68 -2.01R R denotes an observation with a large standardized residual
Conclusions:
There is strong evidence (P < 0.001) that the relationship between strength and % cotton is not linear over the range of % cotton studied. We could try fitting a quadratic relationship (but that won't be on the exam). Since the relationship is not linear the slope of the fitted line has no meaning, so we do not test the slope. Note that the nonlinearity is obvious just by looking at the graph.
Assumptions:
Independent observations; variation in strength follows a normal distribution with the same variance at each level of % cotton.
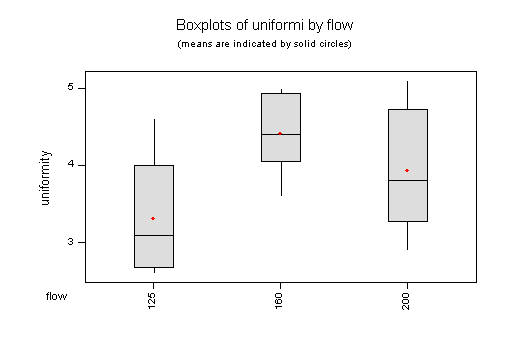
(Note that for exam purposes, a comparative dot plot would be better than a comparative box plot.)
One-way Analysis of Variance
Analysis of Variance for uniformi
Source DF SS MS F P
flow 2 3.648 1.824 3.59 0.053
Error 15 7.630 0.509
Total 17 11.278
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev --+---------+---------+---------+----
125 6 3.3167 0.7600 (-------*--------)
160 6 4.4167 0.5231 (--------*--------)
200 6 3.9333 0.8214 (--------*--------)
--+---------+---------+---------+----
Pooled StDev = 0.7132 2.80 3.50 4.20 4.90
95% Confidence interval for s2: (0.278, 1.22)
Conclusions:
There is some evidence (P = 0.053) that C2F6 flow affects the mean uniformity. Note that the result is not, strictly speaking, significant by a test at the 5% level but it is very close to 5%. A 5% test would accept the hypothesis of no difference due to C2F6 flow.
Assumptions:
Independent observations; variation in compressive strength follows a normal distributionwith the same variance at each level of C2F6 flow.

(Note that for exam purposes, a comparative dot plot would be better than a comparative box plot.)
One-way Analysis of Variance
Analysis of Variance for compress
Source DF SS MS F P
mixing 3 489740 163247 12.73 0.000
Error 12 153908 12826
Total 15 643648
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ---+---------+---------+---------+---
1 4 2971.0 120.6 (------*-----)
2 4 3156.3 136.0 (-----*-----)
3 4 2933.8 108.3 (-----*-----)
4 4 2666.3 81.0 (-----*-----)
---+---------+---------+---------+---
Pooled StDev = 113.3 2600 2800 3000 3200
95% Confidence interval for s2: (6595, 34949)
Conclusions:
There is strong evidence (P < 0.001) that mixing technique affects the compressive strength of concrete. Mixing technique 4 gave a lower mean compressive strength than the others.
Assumptions:
Independent observations; variation in compressive strength follows a normal distribution with the same variance under each mixing technique.
Two-way Analysis of Variance Analysis of Variance for life Source DF SS MS F P material 2 10684 5342 7.91 0.002 temp 2 39119 19559 28.97 0.000 Interaction 4 9614 2403 3.56 0.019 Error 27 18231 675 Total 35 77647 95% Confidence interval for s2: (422, 1251)
Conclusions:
There is some evidence (P = 0.019) that battery material and ambient temperature interact; that is, they both affect battery life but the effect of ambient temperature is different with different materials. Even if we ignore the interaction, there is strong evidence that ambient temperature (P < 0.001) and battery material (P = 0.002) separately affect battery life.
Assumptions:
Independent observations; variation in battery life follows a normal distribution with the same variance at each combination of battery material and ambient temperature.
Two-way Analysis of Variance Analysis of Variance for finish Source DF SS MS F P paint 1 356 356 1.90 0.193 dry_time 2 27 14 0.07 0.930 Interaction 2 1879 939 5.03 0.026 Error 12 2243 187 Total 17 4504 95% Confidence interval for s2: (96.1, 509)
Conclusions:
There is some evidence (P = 0.026) that paint type and dry time interact; that is, they both affect finish but the effect of paint type is different with different dry times. If we were to ignore the interaction, we would say that there is no evidence that dry time (P = 0.930) or paint type (P = 0.193) affect finish, but this conclusion would be misleading.
Assumptions:
Independent observations; variation in finish follows a normal distribution with the same variance at each combination of paint type and dry time.
Two-way Analysis of Variance Analysis of Variance for current Source DF SS MS F P glass 1 14450.0 14450.0 273.79 0.000 phosphor 2 933.3 466.7 8.84 0.004 Interaction 2 133.3 66.7 1.26 0.318 Error 12 633.3 52.8 Total 17 16150.0 95% Confidence interval for s2: (27.1, 144)
Conclusions:
There is no evidence (P = 0.318) that glass type and phosphor type interact, so we can proceed to test the main effects. There is strong evidence that phosphor type (P = 0.004) and glass type (P < 0.001) both affect brightness, and the effect of either one does not depend on the other.
Assumptions:
Independent observations; variation in brightness follows a normal distribution with the same variance at each combination of glass type and phosphor type.