[Binomial-Poisson plot 5, Binomial-Normal plot 5]
The Bin(72, 1/36) distribution has
mean = 72 * (1/36) = 2 variance = 72 * (1/36) (35/36) = 1.9444 standard deviation = sqrt(1.9444) = 1.39443
The first plot compares Bin(72, 1/36) (vertical lines) with Poisson(2) (open dots). The approximation is extremely close. A side-by-side bar plot (e.g. in Excel) would have been a better way to display this but I couldn't figure out how to do it in Minitab.

The second plot compares Bin(72, 1/36) (open dots) with N(2, 1.9444) (+), using overlay plots. The distributions are close but the approximation is very rough. We don't expect the approximation to be good here, since the mean is < 5.
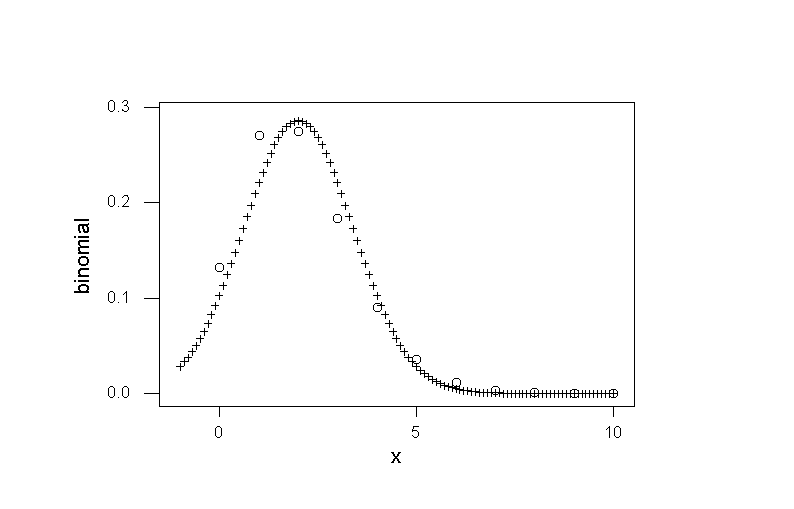
Here are the same distributions, but I used vertical lines for the Binomial and a "line annotation" to add the Normal density as a smooth curve.

PART B - Question 2
[Simulation 8, approximating Normal 4, graph 3]
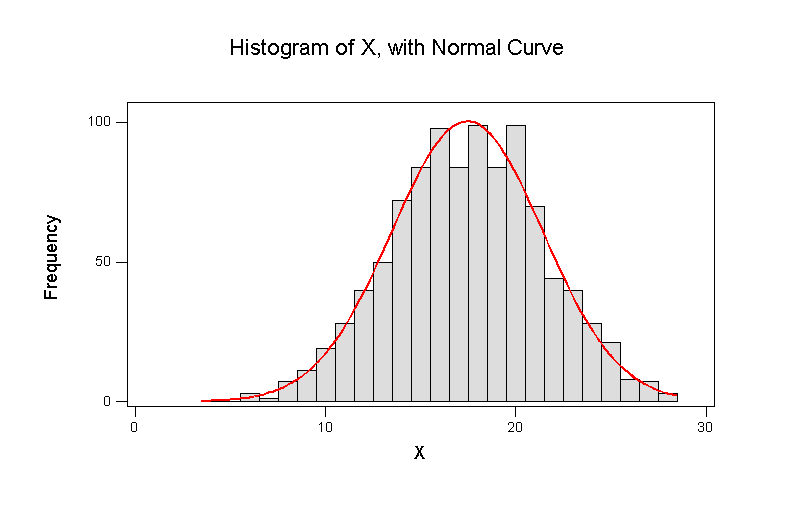
Here is the MINITAB session I ran to set up the discrete distribution (probability 1/6 at each of 1, 2, 3, 4, 5, 6, to simulate one die), then simulate 1000 rolls of 5 dice, compute the total score for each roll, and put the 1000 scores on a histogram with the approximating Normal.
From the formulas derived in 4-112, with a = 1 and b = 6, we have mean = 3.5 and variance = 35/12 = 2.916666 for the score on a single die. Hence for the total score on 5 independent dice
mean = 5 * 3.5 = 17.5 variance = 5 * 35/12 = 175/12 = 14.58333 standard deviation = sqrt(14.58333) = 3.8188
so the approximating Normal distribution is N(17.5, 14.58333).
The simulation gave a sample mean of 17.466 and a sample standard deviation of 3.9707, which are close to the theoretical values. Of course, your simulation results will be close but not exactly the same as mine or anyone else's.
You could compare the histogram of scores with the N(17.5, 14.58333).at the true mean and variance, or the fitted curve N(17.466, 3.97072); I used the default Minitab plot which shows the fitted Normal.
MTB > Set c8 DATA> 1( 1 : 6 / 1 )1 DATA> End. MTB > Set c9 DATA> 6( 1 : 1 / 1 )1 DATA> End. MTB > Let c9 = c9/6 MTB > Random 1000 c1-c5; SUBC> Discrete 'y' 'prob'. MTB > RSum c1-c5 c6. MTB > Mean 'X'. Mean of X Mean of X = 17.466 MTB > StDev 'X'. Standard Deviation of X Standard deviation of X = 3.9707 MTB > Let k1 = 35/2 MTB > Let k2 = SQRT(5*35/12) MTB > prin k1, k2 Data Display K1 17.5000 K2 3.81881 MTB > Describe 'X'; SUBC> GNHist. Descriptive Statistics: X Variable N Mean Median TrMean StDev SE Mean X 1000 17.466 18.000 17.474 3.971 0.126 Variable Minimum Maximum Q1 Q3 X 6.000 28.000 15.000 20.000 Histogram (with Normal Curve) of X