
These are model solutions. Students will get full marks if they do at least the graphs suggested, reach the main conclusions, and justify their conclusions graphically.
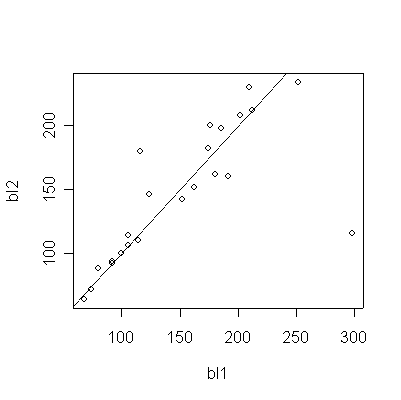
If it takes more than one day of fasting to reduce plasma carotene to suitable base levels, baseline 2 readings will be lower than baseline 1. The scatterplot shows excellent agreement between the two, with points more or less evenly scattered above and below the diagonal, except for subject #71 (in row 1) whose baseline 1 was much higher than baseline 2. The histogram shows that the difference between the two baseline measures is tightly scattered about 0, except for one outlier (subject #71). Hence I would use either baseline 2 or an average of the two, but not baseline 1.


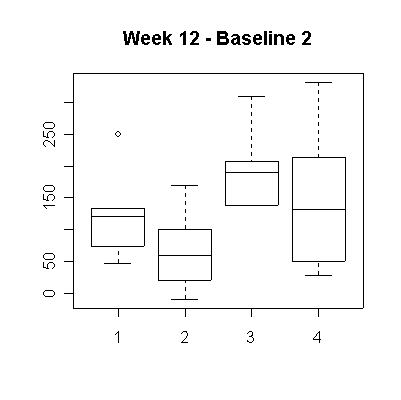
The following box plots of Week 12 minus baseline 1 and minus the mean baseline measure are almost the same. It is clear that Preparation 3 (BASF 30 mg) gives the greatest and most consistent elevation in plasma glucose levels. Preparation 4 (BASF 60 mg) is effective for some people, but overall is less consistent than Preparation 3. Preparation 2 (Roche 60 mg) is consistently the least effective.
 |
 |
There aren't many other graphs I could think of. This one shows the changes over 12 weeks relative to baseline 2 for each subject, with lines coded by preparation. It is not as simple to read as the boxplots. It shows that for most subjects, there was little change between weeks 6 and 12, suggesting that some treatments might achieve steady state levels of plasma carotene in less than 12 weeks.
The box plot of week 6 minus baseline 2 is similar to the boxplot for week 12 minus baseline 2, but the distribution for Preparation 3 is much more variable, suggesting that, for some subjects, Preparation 3 takes more than 6 weeks to achieve its final level.
> attach(betacar)
> windows(h=4,w=4)
> plot(bl1,bl2)
> abline(0,1)
> hist(bl1-bl2)
> boxplot(split(wk12-bl2,prep),main="Week 12 - Baseline 2")
> boxplot(split(wk12-(bl1+bl2)/2,prep),main="Week 12 - Mean Baseline")
> matplot(seq(6,12,by=2),rbind(wk6-bl2,wk8-bl2,wk10-bl2,wk12-bl2),type="l",col=prep,lty=prep,xlab="Week",ylab="Plasma Carotene")
> legend(7,350,paste("Prep",1:4),lty=1:4,col=1:4)
> title("Change from Baseline 2")
> boxplot(split(wk6-bl2,prep),main="Week 6 - Baseline 2")
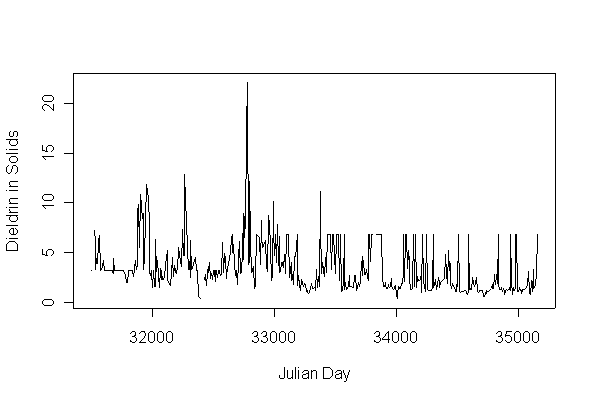
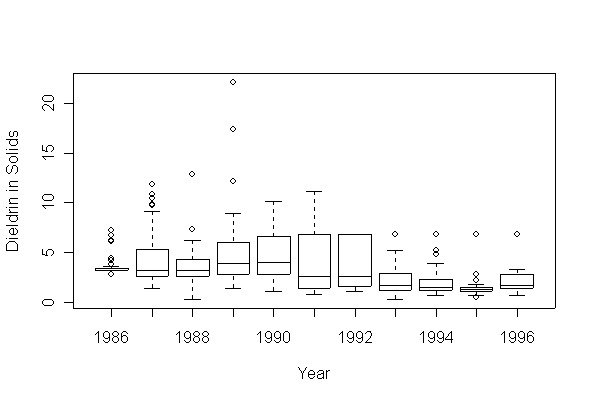
The time series plots show annual cycles throughout and a decreasing trend beginning in 1990. This is reinforced by the boxplots by year. The boxplots by month suggest that highest concentrations of dieldrin in solids are found in the summer months.
The decrease since 1990 shows mostly in a decreasing minimum value, and since this is a very low concentration, the downward trend is much more evident on a log scale. The log scale also makes the variation within months much more comparable, that is, the boxplots by month are more uniform in hinge spread on the log scale than in original units.
The detection limits were 3.2 ng/g up to 1989-02-09 and 6.8 ng/g from 1989-05-25. It is clear from the time series plot that the 6.8 ng/g is an upper detection limit, but the 3.2 ng/g could be either an upper limit or a lower limit as there are both higher and lower values recorded in the same time period.
While the upper detection limits prevent us from seeing if the extreme high values are decreasing after 1989, it is still evident that the bottom of the annual cycle is getting lower.
Because extreme high values occur only a few times in most years, replacement of extreme high values by upper detection limits will not affect the annual medians and lower quartiles in the box plots by year, provided that the upper detection limits are much higher than the annual medians. This is the case from May 1989 onward, where the upper detection limit is 6.8 ng/g.



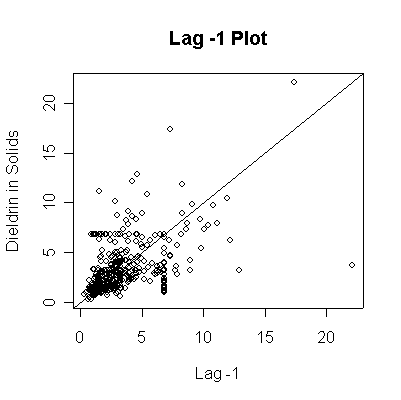
The Lag -1 plot shows moderate autocorrelation; on the log scale, the extreme high values have less impact and the scatter is more elliptical. The upper detection limits show as horizontal and vertical lines in the scatterplot.
 |
 |
> attach(diesol)
> windows(h=4,w=6)
> plot(julian,die.sol,type="l",xlab="Julian Day",ylab="Dieldrin in Solids")
> plot(julian,die.sol,type="l",xlab="Julian Day",ylab="Dieldrin in Solids",log="y")
> boxplot(split(die.sol,year),xlab="Year",ylab="Dieldrin in Solids")
> boxplot(split(die.sol,year),xlab="Year",ylab="Dieldrin in Solids",log="y")
> months <- c("Jan","Feb","Mar","Apr","May","Jun","Jul","Aug","Sep","Oct","Nov","Dec")
> boxplot(split(die.sol,month)[months],ylab="Dieldrin in Solids")
> boxplot(split(die.sol,month)[months],ylab="Dieldrin in Solids",log="y")
> windows(h=4,w=4)
> plot(die.sol[-length(die.sol)],die.sol[-1],xlab="Lag -1",ylab="Dieldrin in Solids",main="Lag -1 Plot")
> abline(0,1)
> plot(die.sol[-length(die.sol)],die.sol[-1],xlab="Lag -1",ylab="Dieldrin in Solids",main="Lag -1 Plot on Log Scale",log="xy")
> abline(0,1)
> diesol[dl,]
julian year month day die.sol dl
1 31504 1986 Apr 2 3.2 TRUE
2 31511 1986 Apr 9 3.2 TRUE
6 31539 1986 May 7 3.2 TRUE
11 31574 1986 Jun 11 3.2 TRUE
12 31588 1986 Jun 25 3.2 TRUE
15 31610 1986 Jul 17 3.2 TRUE
16 31617 1986 Jul 24 3.2 TRUE
17 31624 1986 Jul 31 3.2 TRUE
18 31631 1986 Aug 7 3.2 TRUE
19 31638 1986 Aug 14 3.2 TRUE
20 31645 1986 Aug 21 3.2 TRUE
21 31652 1986 Aug 28 3.2 TRUE
22 31659 1986 Sep 4 3.2 TRUE
23 31665 1986 Sep 10 3.2 TRUE
24 31673 1986 Sep 18 3.2 TRUE
27 31694 1986 Oct 9 3.2 TRUE
28 31701 1986 Oct 16 3.2 TRUE
29 31708 1986 Oct 23 3.2 TRUE
30 31715 1986 Oct 30 3.2 TRUE
31 31722 1986 Nov 6 3.2 TRUE
32 31730 1986 Nov 14 3.2 TRUE
33 31737 1986 Nov 21 3.2 TRUE
34 31743 1986 Nov 27 3.2 TRUE
35 31750 1986 Dec 4 3.2 TRUE
36 31757 1986 Dec 11 3.2 TRUE
37 31764 1986 Dec 18 3.2 TRUE
41 31806 1987 Jan 29 3.2 TRUE
42 31813 1987 Feb 5 3.2 TRUE
43 31820 1987 Feb 12 3.2 TRUE
44 31827 1987 Feb 19 3.2 TRUE
45 31834 1987 Feb 26 3.2 TRUE
46 31841 1987 Mar 5 3.2 TRUE
50 31870 1987 Apr 3 3.2 TRUE
59 31932 1987 Jun 4 3.2 TRUE
65 31981 1987 Jul 23 3.2 TRUE
67 31995 1987 Aug 6 3.2 TRUE
69 32009 1987 Aug 20 3.2 TRUE
79 32079 1987 Oct 29 3.2 TRUE
89 32191 1988 Feb 18 3.2 TRUE
99 32297 1988 Jun 3 3.2 TRUE
103 32324 1988 Jun 30 3.2 TRUE
105 32366 1988 Aug 11 3.2 TRUE
106 32373 1988 Aug 18 3.2 TRUE
123 32499 1988 Dec 22 3.2 TRUE
124 32507 1988 Dec 30 3.2 TRUE
126 32520 1989 Jan 12 3.2 TRUE
127 32527 1989 Jan 19 3.2 TRUE
129 32541 1989 Feb 2 3.2 TRUE
130 32548 1989 Feb 9 3.2 TRUE
141 32653 1989 May 25 6.8 TRUE
169 32856 1989 Dec 14 6.8 TRUE
173 32898 1990 Jan 25 6.8 TRUE
188 33010 1990 May 17 6.8 TRUE
201 33101 1990 Aug 16 6.8 TRUE
202 33108 1990 Aug 23 6.8 TRUE
203 33115 1990 Aug 30 6.8 TRUE
212 33185 1990 Nov 8 6.8 TRUE
244 33437 1991 Jul 18 6.8 TRUE
245 33444 1991 Jul 25 6.8 TRUE
246 33451 1991 Aug 1 6.8 TRUE
247 33458 1991 Aug 8 6.8 TRUE
249 33472 1991 Aug 22 6.8 TRUE
250 33479 1991 Aug 29 6.8 TRUE
251 33486 1991 Sep 5 6.8 TRUE
253 33507 1991 Sep 26 6.8 TRUE
254 33514 1991 Oct 3 6.8 TRUE
255 33521 1991 Oct 10 6.8 TRUE
256 33528 1991 Oct 17 6.8 TRUE
258 33542 1991 Oct 31 6.8 TRUE
262 33570 1991 Nov 28 6.8 TRUE
290 33773 1992 Jun 18 6.8 TRUE
291 33780 1992 Jun 25 6.8 TRUE
293 33794 1992 Jul 9 6.8 TRUE
294 33801 1992 Jul 16 6.8 TRUE
295 33808 1992 Jul 23 6.8 TRUE
297 33815 1992 Jul 30 6.8 TRUE
299 33829 1992 Aug 13 6.8 TRUE
301 33836 1992 Aug 20 6.8 TRUE
302 33843 1992 Aug 27 6.8 TRUE
303 33850 1992 Sep 3 6.8 TRUE
304 33857 1992 Sep 10 6.8 TRUE
305 33864 1992 Sep 17 6.8 TRUE
306 33871 1992 Sep 24 6.8 TRUE
307 33878 1992 Oct 1 6.8 TRUE
331 34060 1993 Apr 1 6.8 TRUE
333 34074 1993 Apr 15 6.8 TRUE
334 34081 1993 Apr 22 6.8 TRUE
342 34137 1993 Jun 17 6.8 TRUE
345 34158 1993 Jul 8 6.8 TRUE
353 34214 1993 Sep 2 6.8 TRUE
357 34242 1993 Sep 30 6.8 TRUE
365 34298 1993 Nov 25 6.8 TRUE
391 34509 1994 Jun 24 6.8 TRUE
402 34592 1994 Sep 15 6.8 TRUE
430 34830 1995 May 11 6.8 TRUE
445 34934 1995 Aug 23 6.8 TRUE
451 34977 1995 Oct 5 6.8 TRUE
452 34984 1995 Oct 12 6.8 TRUE
475 35152 1996 Mar 28 6.8 TRUE