Contents
function out = inventories()
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % This code simulates the Inventory Model as specified in % Grasselli and Nguyen-Huu (2018) % % % authors: M. Grasselli and A. Nguyen-Huu %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% clear all close all clc warning off
Base Parameters
This is a combination of Grasselli and Nguyen-Huu (2015) and Giraud and Grasselli (2019)
phi0 = 0.0401; %Phillips curve parameter phi1 = 6.41e-05; %Phillips curve parameter kappa0 = -0.0065; % constant parameter in investment function kappa1 = -5; % affine parameter in exponent of investment function kappa2 = 20; % coefficient in the exponent of investment function eta_u = 0.2; % adjustment speed for investment as function of utilization u_b = 0.9; % baseline utilization c_minus= 0.03; % consumption share hard-lower bound A_c = 0; %Consumption share asymptotic lower bound B_c = 5; % Consumption share growth rate C_c = 1; K_c = 0.9; %Consumption share upper bound nu_c = 0.2; Q_c= ((K_c-A_c)/(c_minus-A_c))^nu_c-C_c;
Other definitions
TOL = 1E-7; options = odeset('RelTol', TOL); txt_format = '%3.3g';
Functions of interest
inflation = @(x1,x2,x3) eta_p*(markup*x1-1)+eta_q*(x2-x3); % inflation, equation (31) phillips = @(x) phi1./(1-x).^2- phi0; % Phillips curve, equation (32) phillips_prime = @(x) 2*phi1./(1-x).^3; % derivative of phillips curve phillips_inv = @(x) 1 - (phi1./(x+phi0)).^(1/2); % inverse of phillips curve investment= @(x1,x2) kappa0+exp(kappa1+kappa2.*x1)+eta_u*(x2-u_b); % investment function, equation (25) % consumption, equation (24) with generalised logistic function depending % on income only consumption =@(x) max(c_minus,A_c + ((K_c-A_c)./(C_c+Q_c*exp(-B_c*x)).^(1/nu_c))); consumption_inv = @(x) -log((((K_c-A_c)./(x-A_c)).^nu_c-C_c)./Q_c)./B_c; % inverse of the consumption function over positive income
Example 1
nu = 3; % capital to output ratio alpha = 0.025; % productivity growth rate beta = 0.02; % population growth rate delta = 0.05; % depreciation rate r = 0.03; % real interest rate eta_p = 0.8; % adjustment speed for prices with respect to cost eta_q = 0.2; % adjustment speed for prices with respect to demand eta_e = 0.8; % adjustment speed for expected sales eta_d = 0.7; % adjustment speed for desired inventory markup = 1.2; % mark-up value gamma = 0.4; % (1-gamma) is the degree of money illusion f_d = 0.1; % desired inventories as a fraction of expected sales % Functions of interest inflation = @(x1,x2,x3) eta_p*(markup*x1-1)+eta_q*(x2-x3); % inflation, equation (31) phillips = @(x) phi1./(1-x).^2- phi0; % Phillips curve, equation (32) phillips_prime = @(x) 2*phi1./(1-x).^3; % derivative of phillips curve phillips_inv = @(x) 1 - (phi1./(x+phi0)).^(1/2); % inverse of phillips curve investment= @(x1,x2) kappa0+exp(kappa1+kappa2.*x1)+eta_u*(x2-u_b); % investment function, equation (25) % consumption, equation (24) with generalised logistic function depending % on income only consumption =@(x) max(c_minus,A_c + ((K_c-A_c)./(C_c+Q_c*exp(-B_c*x)).^(1/nu_c))); consumption_inv = @(x) -log((((K_c-A_c)./(x-A_c)).^nu_c-C_c)./Q_c)./B_c; % inverse of the consumption function over positive income % Numerical Values of Interest ydbar = 1/(1+(alpha+beta)*f_d); yebar = 1/(1+(alpha+beta)*f_d) x=fsolve(@system2d, [0.9,0.1]); omegabar=x(1) dbar=x(2) ibar=inflation(omegabar,ydbar,yebar); ubar=(nu*(alpha+beta+delta)*(1+(alpha+beta)*f_d))/(1-consumption(omegabar)*(1+(alpha+beta)*f_d)) kbar=investment(yebar*(1-omegabar)-r*dbar,ubar); cbar = consumption(omegabar); lambdabar = phillips_inv(alpha+(1-gamma)*ibar) % Sample paths of the Keen model with inventories omega0 = 0.9; lambda0 = 0.9; d0 = 0.5; ye0 = 0.9; u0 = 0.8; y0=[convert([omega0, lambda0]),d0,ye0,u0]; Y0 = 100; T = 200; [tK,yK] = ode15s(@(t,y) keen_inventory(y), [0 T], y0, options); sol = retrieve([yK(:,1),yK(:,2)]); yK(:,1)=sol(:,1); yK(:,2)=sol(:,2); Y_output = Y0*yK(:,2)/lambda0.*exp((alpha+beta)*tK); n=length(yK(:,3)); omega_eq = yK(n,1) lambda_eq = yK(n,2) d_eq = yK(n,3) ye_eq = yK(n,4) u_eq = yK(n,5) figure(1) plot(yK(:,1), yK(:,2)), hold on; %plot(bar_omega_K, bar_lambda_K, 'ro') xlabel('\omega') ylabel('\lambda') title(['\omega_0 = ', num2str(omega0, txt_format), ... ', \lambda_0 = ', num2str(lambda0, txt_format), ... ', d_0 = ', num2str(d0, txt_format), ... ', Y_0 = ', num2str(Y0, txt_format)]) % print('dual_keen_phase_convergent','-depsc') figure(2) yyaxis right plot(tK, yK(:,1),tK,yK(:,2),tK,yK(:,4),tK,yK(:,5)) ylabel('\omega,\lambda,y_e,u') yyaxis left plot(tK, yK(:,3)) ylabel('d') title(['\omega_0 = ', num2str(omega0,txt_format), ... ', \lambda_0 = ', num2str(lambda0, txt_format), ... ', ye_0 = ', num2str(ye0, txt_format), ... ', u_0 = ', num2str(u0, txt_format)]) legend('d','\omega', '\lambda','y_e','u') % print('dual_keen_time_convergent','-depsc')
yebar =
0.9955
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.
omegabar =
0.8522
dbar =
0.3503
ubar =
1.8399
lambdabar =
0.9710
omega_eq =
0.8521
lambda_eq =
0.9710
d_eq =
0.3503
ye_eq =
0.9955
u_eq =
1.8399
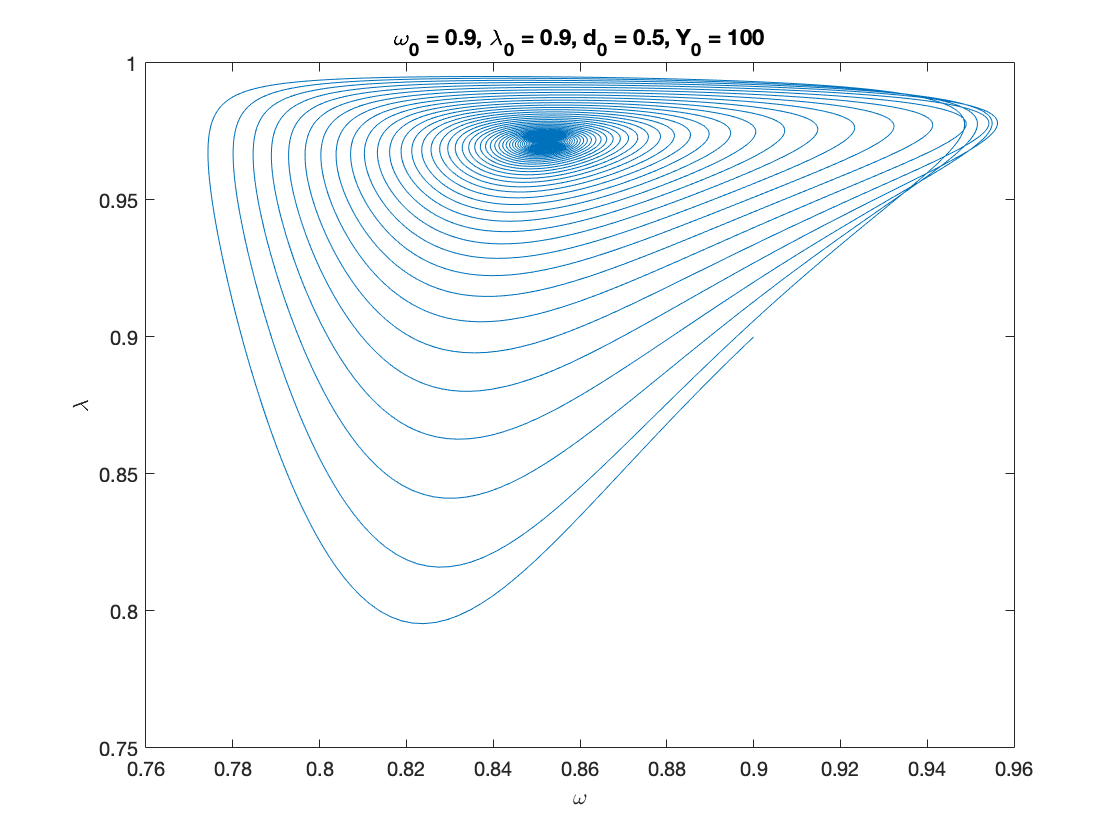
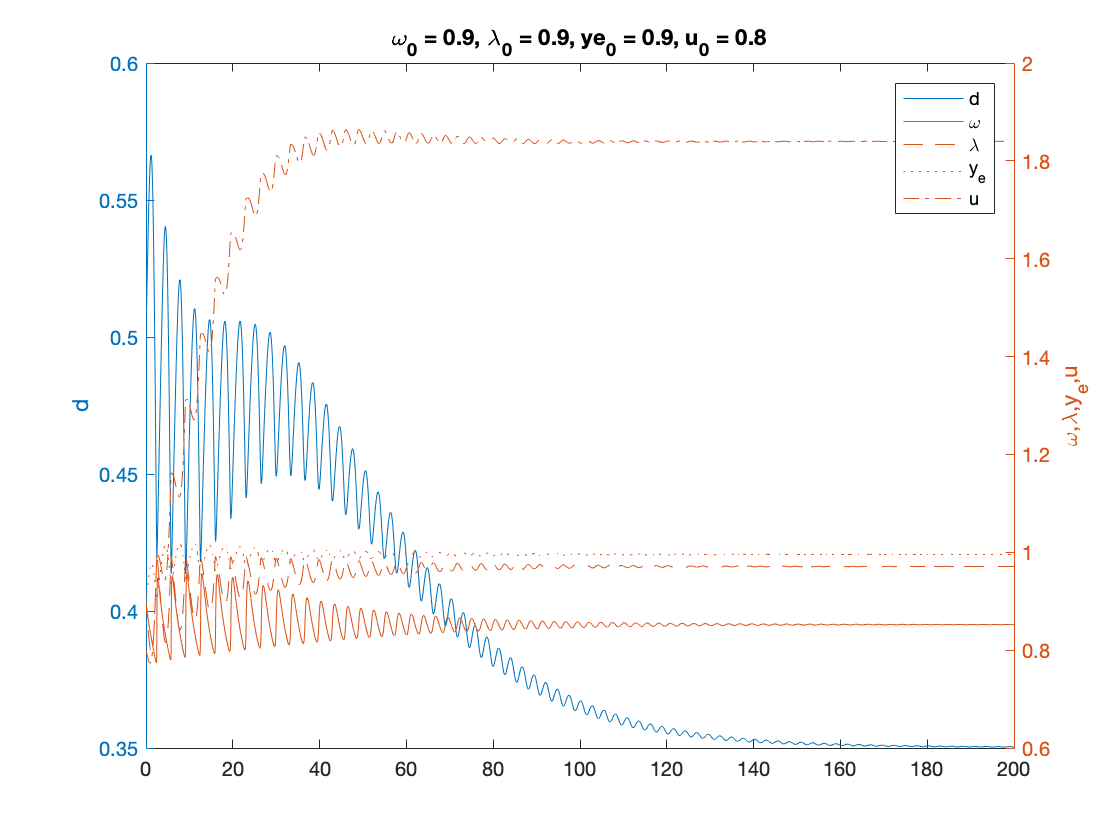
Auxiliary functions
Instead of integrating the system in terms of omega, lambda and d, we decided to use:
log_omega = log(omega), tan_lambda = tan((lambda-0.5)*pi), and y_h=omega-r*d disposable income of households
Experiments show that the numerical methods work better with these variables.
function new = convert(old) % This function converts % [omega, lambda, d, p] % to % [log_omega, tan_lambda, y] % It also work with the first 2 components alone. % each of these variables might also be a time-dependent vector n = size(old,2); %number of variables new = zeros(size(old)); new(:,1) = log(old(:,1)); new(:,2) = tan((old(:,2)-0.5)*pi); if n>2 new(:,3) = old(:,1)-r.*old(:,3); end end function old = retrieve(new) % This function retrieves [omega, lambda, d, p] % from % [log_omega, tan_lambda, pi_n, log_p] % % It also work with the first 2 or 3 elements alone. % each of these variables might also be a time-dependent vector n = size(new,2); %number of variables old = zeros(size(new)); old(:,1) = exp(new(:,1)); old(:,2) = atan(new(:,2))/pi+0.5; if n>2 old(:,3) = (old(:,1)-new(:,3))./r; end end function f = keen_inventory(y) f = zeros(5,1); log_omega = y(1); tan_lambda = y(2); d = y(3); ye = y(4); u = y(5); lambda = atan(tan_lambda)/pi+0.5; omega = exp(log_omega); pi_e = ye*(1-omega)-r*d; yd = consumption(omega)+investment(pi_e,u)/u; g_Y = (f_d*(alpha+beta+eta_d)+1)*(ye*(alpha+beta)+eta_e*(yd-ye))+eta_d*(yd-1); f(1) = phillips(lambda)-alpha-(1-gamma)*inflation(omega,yd,ye); %d(log_omega)/dt f(2) = (1+tan_lambda^2)*pi*lambda*(g_Y-alpha-beta); %d(tan_lambda)/dt f(3) = d*(r-g_Y-inflation(omega,yd,ye))+omega-consumption(omega); %d(d)/dt f(4) = ye*(alpha+beta-g_Y)+eta_e*(yd-ye); % dy_e/dt f(5) = u*(g_Y-investment(pi_e,u)/nu+delta); % du/dt end function F = system2d(x) F(1) = investment(yebar*(1-x(1))-r*x(2),(nu*(alpha+beta+delta)*(1+(alpha+beta)*f_d))/(1-consumption(x(1))*(1+(alpha+beta)*f_d))) - nu*(alpha+beta+delta); F(2) = x(2) - (x(1)-consumption(x(1)))/(alpha+beta+inflation(x(1),ydbar,yebar)-r); end
end